Keyword [Batch SGM] [Feature Regularization]
Hariharan B, Girshick R. Low-shot visual recognition by shrinking and hallucinating features[C]//Proceedings of the IEEE International Conference on Computer Vision. 2017: 3018-3027.
1. Overview
1.1. Motivation
- The transformation between two samples among the same category (base class), can be apply to few samples among the same category (novel class) to hallucinate more samples.

In this paper, it proposes
- Feature representation regularization techniques.
- Hallucinate additional training exmaples for data-starved classes.

1.2. Procedure
1) Representation Learning (training phase one)
2) Low-shot learning (training phase two)
3) Testing
2. Details
2.1. Hallucination
1) Any two exmaplses $z_1$ and $z_2$ belonging to the same category represent a plausible transformation.
2) Given a novel category example $x$, apply to $x$ the transformation that sent $z_1$ to $z_2$.
3) By doing this, train function $G([\phi (x), \phi (z_1), \phi (z_2)])$ which output hallucinated feature vertor. ($\phi$ is feature extractor. And use MLP with 3 FC for $G$)
Steps
1) Cluster feature vectors ($\phi (z)$) of exmaples in each base category into a fixed number of cluster (100).
2) For each pair of centroids $c_1^a, c_2^a$ in one category $a$, search for another pair of centroids $c_1^b, c_2^b$ form another category $b$. Such that the cosine distance between $c_1^a-c_2^a$ and $c_1^b-c_2^b$ is minimized.
3) Collect all such quadruplets $(c_1^a, c_2^a, c_1^b, c_2^b)$ with cosine similarity greater than zero into a dataset $D_G$.
4) To train $G$, feed $(c_1^a, c_1^b, c_2^b)$ to $G$, then $\hat{c}_2^a=G([c_1^a, c_1^b, c_2^b])$. And minimize $\lambda L_{mse}(\hat{c}_2^a, c_2^a) + L_{cls}(W, \hat{c}_2^a, a)$
2.2. Feature Representaion Regularization
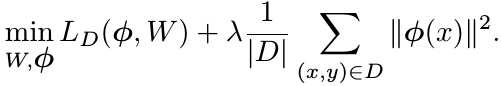
1) When learning classifier and feature extractor jointly, the feature extractor choose to encode less discriminative information in the feature vector, because the classifier can learn to ignore this information.
2) When learning new classifier in the low-show space, the learner will not have enough data to identify discriminative features for the unseen classes form its representation.
3) Minimizing the norm of the feature activations might limit what the learner can encode into the features, and thus force it to only encode useful information.